はじめに¶
この記事は理研 R-CCS の辻さんの行ったチューニングを再現しながら富岳のためのチューニング事例としたものです。オリジナルの文献としては [1] (日本語)、及び [2] を御参照ください。
どんな計算をしているか¶
今回紹介するコードは、 axhelm というスペクトル要素法のカーネル部となります。これはある種の高次の有限要素法で、六面体要素の中に 83 個の選点を持つものです。正確には次数は可変ですが、今回は倍精度の SIMD 長である 8 に固定してチューニングを進めています。
それぞれの軸方向のベクトルに 8×8 の行列を掛けることで勾配が求まります。この箇所は 84 の4重ループとなります( loop-2a )。
次にこの勾配に 3×3 の対称行列の幾何係数を掛けます。幾何係数の役割は、密度と体積要素で重みを取ること、六面体の内部座標での勾配を外部のユークリッド座標での勾配に変換することです。 3×3 対称行列に関しては手動で展開して書かれているので、この箇所は 83 の3重ループとなります( loop-2b )。
実際には loop-2a と loop-2b は融合して書かれており、中間変数の領域を節約しています。ここから loop-3 へと行く間には 3×83 語の中間変数が発生しています。 12 KiB なので L1 キャッシュ( 64 KiB )に十分収まります。
最後に最初に使った勾配行列の転置を掛けます( loop-3 )。
数式で書くと、行列
を作用させ \(A \vec{u}\) を計算しているというカーネルになります。勾配の転置を掛ける意味がわかりにくいかもしれませんが、次のように定義された内積
の計算に対して最後の \(\vec v^T\) を掛ける部分だけ省いたものになっています。 より詳しい定式化については [3] をご参照ください。
全体の流れ¶
この記事では "as-is" の tune-0 から始め、 tune-1 では SIMD 化を改善します。 tune-2 では連続アクセス化によるギャザー命令の回避を行い、 tune-3 ではループの collapse を行うことでソフトウェアパイプライニングを促進します。 最後に tune-4 で、プリフェッチ命令の挿入を促進させメモリアクセス性能を向上させます。途中 tune-1a で、 tune-1 と同等の SIMD 化をディレクティブを用いずに行う方法も紹介します。
As-is での性能 (tune-0)¶
49extern "C" void axhelm_bk_v0(
50 dlong Nelements, // dlong=int, dfloat=double
51 const dlong & offset, // not used
52 const dfloat* __restrict__ ggeo, // [Nelements][7][8][8][8]
53 const dfloat* __restrict__ D, // [8][8]
54 const dfloat* __restrict__ lambda, // not used
55 const dfloat* __restrict__ q, // [Nelements][8][8][8]
56 dfloat* __restrict__ Aq ) // [Nelements][8][8][8]
57{
58 dfloat s_q [p_Nq][p_Nq][p_Nq]; // #define p_Nq 8
59 dfloat s_Gqr[p_Nq][p_Nq][p_Nq];
60 dfloat s_Gqs[p_Nq][p_Nq][p_Nq];
61 dfloat s_Gqt[p_Nq][p_Nq][p_Nq];
62
63 dfloat s_D[p_Nq][p_Nq];
64
65 for(int j = 0; j < p_Nq; ++j)
66 for(int i = 0; i < p_Nq; ++i)
67 s_D[j][i] = D[j * p_Nq + i];
68
69#pragma omp parallel for private(s_q, s_Gqr, s_Gqs, s_Gqt) firstprivate(s_D)
70 for(dlong e = 0; e < Nelements; ++e) {
71 const dlong element = e;
72 for(int k = 0; k < p_Nq; ++k) for(int j = 0; j < p_Nq; ++j) // loop-1
73 for(int i = 0; i < p_Nq; ++i) {
74 const dlong base = i + j * p_Nq + k * p_Nq * p_Nq + element * p_Np;
75 const dfloat qbase = q[base];
76 s_q[k][j][i] = qbase;
77 }
78
79 for(int k = 0; k < p_Nq; ++k) for(int j = 0; j < p_Nq; ++j) // loop-2
80 {
81 for(int i = 0; i < p_Nq; ++i) {
82 // const dlong id = i + j * p_Nq + k * p_Nq * p_Nq + element * p_Np;
83 const dlong gbase = element * p_Nggeo * p_Np + k * p_Nq * p_Nq + j * p_Nq + i;
84 const dfloat r_G00 = ggeo[gbase + p_G00ID * p_Np]; // #define p_G00ID 1
85 const dfloat r_G01 = ggeo[gbase + p_G01ID * p_Np]; // #define p_G01ID 2
86 const dfloat r_G11 = ggeo[gbase + p_G11ID * p_Np]; // #define p_G11ID 3
87 const dfloat r_G12 = ggeo[gbase + p_G12ID * p_Np]; // #define p_G12ID 4
88 const dfloat r_G02 = ggeo[gbase + p_G02ID * p_Np]; // #define p_G02ID 5
89 const dfloat r_G22 = ggeo[gbase + p_G22ID * p_Np]; // #define p_G22ID 6
90
91 dfloat qr = 0.f;
92 dfloat qs = 0.f;
93 dfloat qt = 0.f;
94 // loop-2a (gradient)
95 for(int m = 0; m < p_Nq; ++m) {
96 qr += s_D[i][m] * s_q[k][j][m];
97 qs += s_D[j][m] * s_q[k][m][i];
98 qt += s_D[k][m] * s_q[m][j][i];
99 }
100 // loop-2b (geometry factor)
101 s_Gqr[k][j][i] = r_G00 * qr + r_G01 * qs + r_G02 * qt;
102 s_Gqs[k][j][i] = r_G01 * qr + r_G11 * qs + r_G12 * qt;
103 s_Gqt[k][j][i] = r_G02 * qr + r_G12 * qs + r_G22 * qt;
104 }
105 }
106
107 for(int k = 0; k < p_Nq; ++k) for(int j = 0; j < p_Nq; ++j) // loop-3 (grad^T)
108 {
109 for(int i = 0; i < p_Nq; ++i) {
110 const dlong id = element * p_Np + k * p_Nq * p_Nq + j * p_Nq + i;
111 dfloat r_Aqr = 0, r_Aqs = 0, r_Aqt = 0;
112
113 for(int m = 0; m < p_Nq; ++m) {
114 r_Aqr += s_D[m][i] * s_Gqr[k][j][m];
115 r_Aqs += s_D[m][j] * s_Gqs[k][m][i];
116 r_Aqt += s_D[m][k] * s_Gqt[m][j][i];
117 }
118
119 Aq[id] = r_Aqr + r_Aqs + r_Aqt;
120 }
121 }
122 }
123}
富士通コンパイラ
4.8.0 (tcsds-1.2.35)
の
trad
モードにオプション
-Kfast,openmp,ocl,optmsg=2
でコンパイルし
2.0 GHz
で実行したところ、
1
ノードあたり
126 GFLOP/s
となりました。ノードあたりの
MPI
プロセスは
4
、プロセスあたりのスレッドは
12
という標準的な組み合わせを用いました。問題サイズは
7680
要素です。なお、
GFLOP/s
値は理論演算数からプログラムの内部で求めているため、プロファイラの出力するものとは若干ずれることがあります。
ここからは、まず最初 SIMD 化について検討してみます。
SIMD 化 (tune-1)¶
先程のコードでコンパイラは次のような最適化メッセージを出力しています(抜粋):
jwd8222o-i "axhelm-0.cpp", line 78: このループで必要なプリフェッチの数が、ハードウェアプリフェッチの許容数を超えたため、prefetch命令を生成しました。
jwd8662o-i "axhelm-0.cpp", line 78: スケジューリング結果を得られなかったため、ソフトウェアパイプライニングを抑止しました。
jwd8203o-i "axhelm-0.cpp", line 80: このループをフルアンローリングしました。
jwd6004s-i "axhelm-0.cpp", line 94: リダクション演算を含むループ制御変数'm'のループをSIMD化しました。
jwd8209o-i "axhelm-0.cpp", line 100: 多項式の演算順序を変更しました。
jwd8668o-i "axhelm-0.cpp", line 106: 命令数が多いため、ソフトウェアパイプライニングを抑止しました。
jwd8203o-i "axhelm-0.cpp", line 106: このループをフルアンローリングしました。
jwd8203o-i "axhelm-0.cpp", line 108: このループをフルアンローリングしました。
jwd6004s-i "axhelm-0.cpp", line 112: リダクション演算を含むループ制御変数'm'のループをSIMD化しました。
最内側ループの添字
m
に対してコンパイラの
SIMD
化が適用されたことがわかります。最内側のループに対してベクトル化を行うのは多くのコンパイラにとって標準的な挙動ですが、以下の理由からこれは最適な
SIMD
化とはいえません:
長さが 8 のベクトル同士の内積の計算に 1 回の乗算と 1 回の水平加算の命令となってしまい演算効率が悪い(十分に長いベクトル同士の内積であれば SIMD の積和命令を繰り返し最後に水平和を取るという方法も有効)
勾配の計算のみが SIMD 化され幾何係数を掛ける部分が一切 SIMD 化されない
このため最内側のループ変数
m
に対してではなくそのひとつ外側の
i
に対して
SIMD
化を行うというのが目指す方向となります。簡単にこれを実現するのは最内側の
m-loop
をアンロールしてしまうことで、手動アンロールしなくてもコンパイラ提供のディレクティブを使って以下のように書けます:
94#pragma loop fullunroll_pre_simd
95 for(int m = 0; m < p_Nq; ++m) {
96 qr += s_D[i][m] * s_q[k][j][m];
97 qs += s_D[j][m] * s_q[k][m][i];
98 qt += s_D[k][m] * s_q[m][j][i];
99 }
113#pragma loop fullunroll_pre_simd
114 for(int m = 0; m < p_Nq; ++m) {
115 r_Aqr += s_D[m][i] * s_Gqr[k][j][m];
116 r_Aqs += s_D[m][j] * s_Gqs[k][m][i];
117 r_Aqt += s_D[m][k] * s_Gqt[m][j][i];
118 }
このように最内側の m-loop を 2 箇所アンロールすることで、コンパイラはそのひとつ外側の i-loop に対して SIMD 化を行います。実際にコンパイラは次のようなメッセージを出力します:
jwd8203o-i "axhelm-1.cpp", line 71: このループをフルアンローリングしました。
jwd6001s-i "axhelm-1.cpp", line 72: ループ制御変数'i'のループをSIMD化しました。
jwd8668o-i "axhelm-1.cpp", line 78: 命令数が多いため、ソフトウェアパイプライニングを抑止しました。
jwd8203o-i "axhelm-1.cpp", line 78: このループをフルアンローリングしました。
jwd6001s-i "axhelm-1.cpp", line 80: ループ制御変数'i'のループをSIMD化しました。
jwd8203o-i "axhelm-1.cpp", line 95: このループをフルアンローリングしました。
jwd8662o-i "axhelm-1.cpp", line 107: スケジューリング結果を得られなかったため、ソフトウェアパイプライニングを抑止しました。
jwd8203o-i "axhelm-1.cpp", line 107: このループをフルアンローリングしました。
jwd6001s-i "axhelm-1.cpp", line 109: ループ制御変数'i'のループをSIMD化しました。
jwd8203o-i "axhelm-1.cpp", line 114: このループをフルアンローリングしました。
この変更により 329 GFLOP/s が得られました。
なお、ディレクティブを用いずに同等のSIMD化を行う変形については 別解 (tune-1a) に載せてあります。
ここで詳細プロファイラによる統計情報と実行時間内訳を tune-0 と比較してみます。
CMG ( 1 MPI プロセス、 12 スレッド)あたりの統計情報は以下のようになります:
Statistics |
Execution
time (s)
|
Gflops |
Floating-
point
operation
peak ratio
(%)
|
Memory
throughput
(GB/s)
|
Memory
throughput
peak ratio
(%)
|
Effective
instruction
|
Floating-
point
operation
|
SIMD
instruction
rate (%)
(/Effective
instruction)
|
SVE
operation
rate (%)
|
Floating-
point
pipeline
Active
element rate
|
IPC |
GIPS |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
Tune-0 |
3.13E-01 |
65.71 |
8.56% |
24.95 |
9.75% |
7.97E+09 |
2.05E+10 |
57.06% |
91.87% |
92.29% |
1.06 |
25.50 |
Tune-1 |
1.09E-01 |
96.30 |
12.54% |
70.31 |
27.42% |
2.08E+09 |
1.05E+10 |
75.41% |
100.0% |
91.77% |
0.79 |
19.06 |
実行時間が最も客観的な指標で、ほぼ 1/3 となっていることがわかります。 Gflops 値は一見あまり伸びていないように見えるのですが、これは tune-0 では水平加算命令のために浮動小数点演算数が本来より多く数えられてしまっているためです。浮動小数点演算数は以降のチューニングでは増えることはありません。全体としては今回の tune-1 によりほぼ全ての浮動小数点演算が SIMD 化されたことで命令数が大幅に減ったことが実行時間の短縮に寄与したものといえます。
実行時間の内訳は以下のようになります:
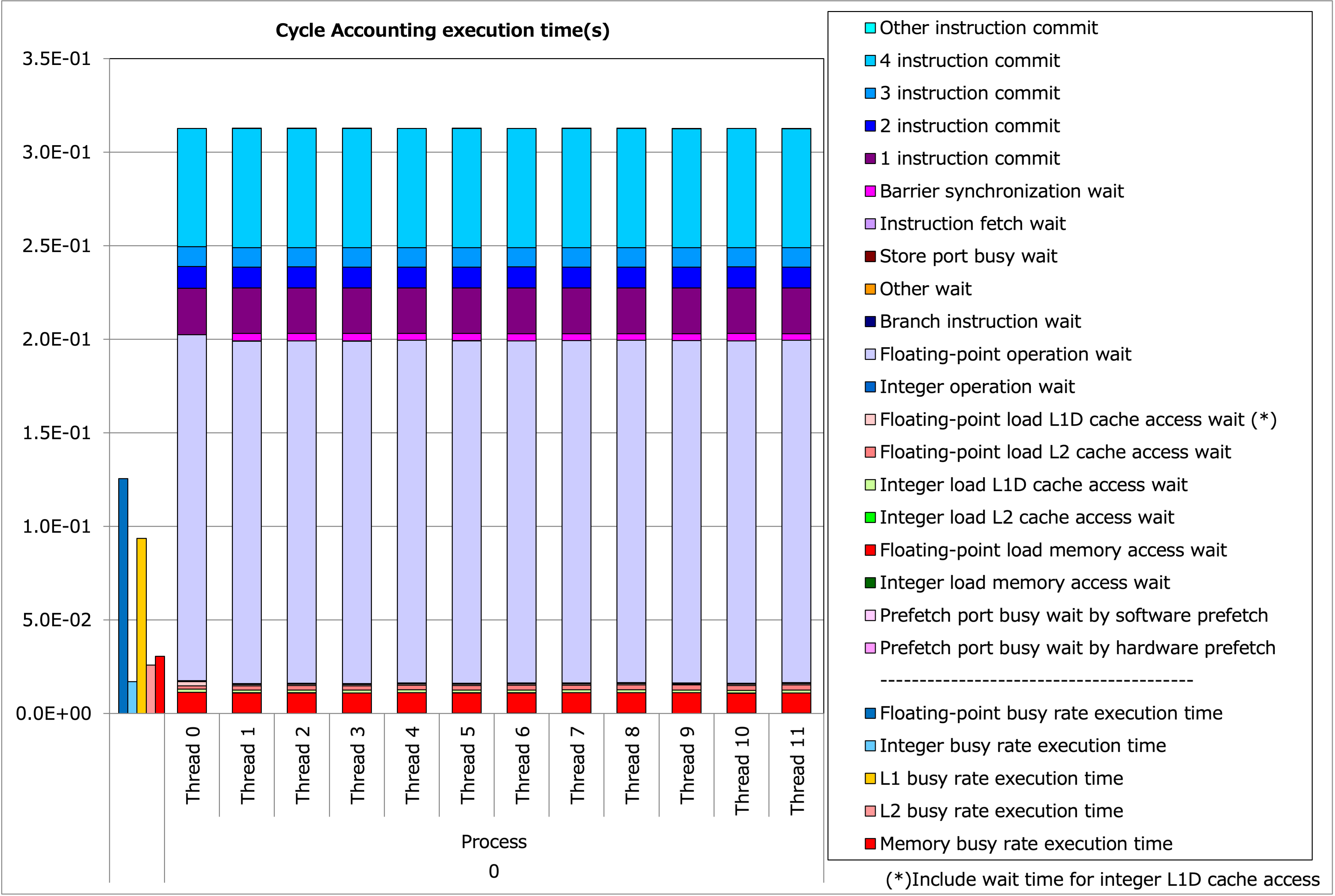
Tune-0 の実行時間内訳¶
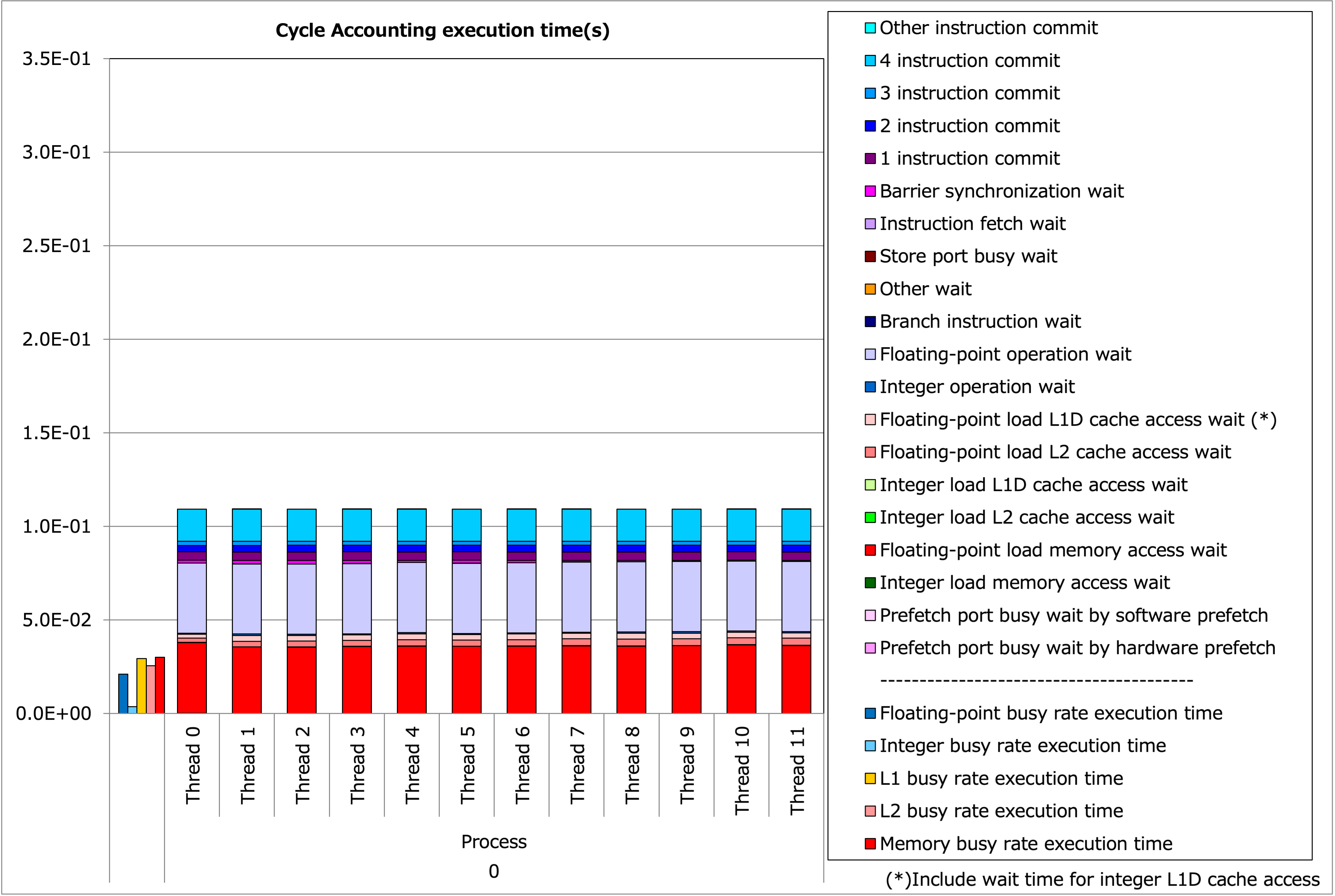
Tune-1 の実行時間内訳¶
命令数そのものが減ったことにより実行時間が短縮されています。ただし、 tune-1 の結果にもまだ改善の余地があります。
連続アクセス化とギャザーの回避 (tune-2)¶
ここまでの SIMD 化で、一部非効率なメモリアクセスが残っています。
95 for(int m = 0; m < p_Nq; ++m) {
96 qr += s_D[i][m] * s_q[k][j][m];
97 qs += s_D[j][m] * s_q[k][m][i];
98 qt += s_D[k][m] * s_q[m][j][i];
99 }
添字
[i]
によるベクトル化なので、この3行は最初がベクトル×スカラーの積、残りの2つがスカラ×ーベクトル積に相当します。最初の行の
s_D[i][m]
は添字に
[i]
を含むのでベクトル化されますが、最内側ではないのでストライドないしギャザーアクセスになってしまいます。実際、コンパイラは次のようなコードを出力しています:
/* 96 */ index z17.d, 0, 8
/* 96 */ ld1d {z16.d}, p0/z, [x16, z17.d, lsl #3] // "s_D"
アセンブリを読むのを避けたいというときは、詳細プロファイラの出力からもギャザー命令が出ていることを確認できます。
Tune-1 の詳細プロファイラ出力¶
幸い、この行列は 8×8 と小さく、要素間での依存もないので関数の入り口で転置を作っておくことができます。実際にそのようなチューニングを行ったのが以下のコードになります:
62 dfloat s_D[p_Nq][p_Nq], s_T[p_Nq][p_Nq];
63
64 for(int j = 0; j < p_Nq; ++j)
65 for(int i = 0; i < p_Nq; ++i){
66 s_D[j][i] = D[j * p_Nq + i];
67 s_T[i][j] = D[j * p_Nq + i];
68 }
69
70#pragma omp parallel for private(s_q, s_Gqr, s_Gqs, s_Gqt) firstprivate(s_D, s_T)
97 for(int m = 0; m < p_Nq; ++m) {
98 qr += s_T[m][i] * s_q[k][j][m];
99 qs += s_D[j][m] * s_q[k][m][i];
100 qt += s_D[k][m] * s_q[m][j][i];
101 }
s_T[i][j]
が
s_D[j][i]
の転置行列となります。この変更で
358 GFLOPS/s
(
tune-1
から
+8.8%
)となりました。
ループ collaps によるソフトウェアパイプライニング (tune-3)¶
i-loop の長さが丁度 SIMD 長の8としてベクトル化された後は、そのひとつ外側の j-loop でソフトウェアパイプライニングのようなスケジューリングを目指すことになります。 ただし(コンパイル時に既知の) j-loop の長さは 8 であり、ソフトウェアパイプライニングを適用するには短すぎるようです。このため現状のコードでは、コンパイラは j-loop をフルアンロールし、既に十分に大きなループボディとなった k-loop に対しては何もしないという選択をしています。
ここでは、 j-loop と k-loop を collapse し長さ 64 のループとすることでより良いスケジューリングが得られるようにします。 ループの collapse は OpemMP によるスレッド並列化の際に最外ループの並列度が十分でないときにディレクティブから行うこともあるやり方ですが、単に collapse するだけのディレクティブは無かったので手動で行うこととします。
84 for(int kj = 0; kj < p_Nq*p_Nq; ++kj) {
85 const int j = kj % p_Nq;
86 const int k = kj / p_Nq;
3 箇所に同様の変更を施しコンパイラの出力メッセージは以下のようになっています:
jwd8204o-i "axhelm-3.cpp", line 73: ループにソフトウェアパイプライニングを適用しました。
jwd8205o-i "axhelm-3.cpp", line 73: ループの繰返し数が64回以上の時、ソフトウェアパイプライニングを適用したループが実行時に選択されます。
jwd6001s-i "axhelm-3.cpp", line 77: ループ制御変数'i'のループをSIMD化しました。
jwd8204o-i "axhelm-3.cpp", line 84: ループにソフトウェアパイプライニングを適用しました。
jwd8205o-i "axhelm-3.cpp", line 84: ループの繰返し数が48回以上の時、ソフトウェアパイプライニングを適用したループが実行時に選択されます。
jwd6001s-i "axhelm-3.cpp", line 88: ループ制御変数'i'のループをSIMD化しました。
jwd8203o-i "axhelm-3.cpp", line 103: このループをフルアンローリングしました。
jwd8204o-i "axhelm-3.cpp", line 115: ループにソフトウェアパイプライニングを適用しました。
jwd8205o-i "axhelm-3.cpp", line 115: ループの繰返し数が48回以上の時、ソフトウェアパイプライニングを適用したループが実行時に選択されます。
jwd6001s-i "axhelm-3.cpp", line 119: ループ制御変数'i'のループをSIMD化しました。
jwd8203o-i "axhelm-3.cpp", line 124: このループをフルアンローリングしました。
この変更で 374 GFLOP/s ( tune-2 から +4.5% )が得られました。
プロファイリングの結果を tune-2 のものと比べてみます。
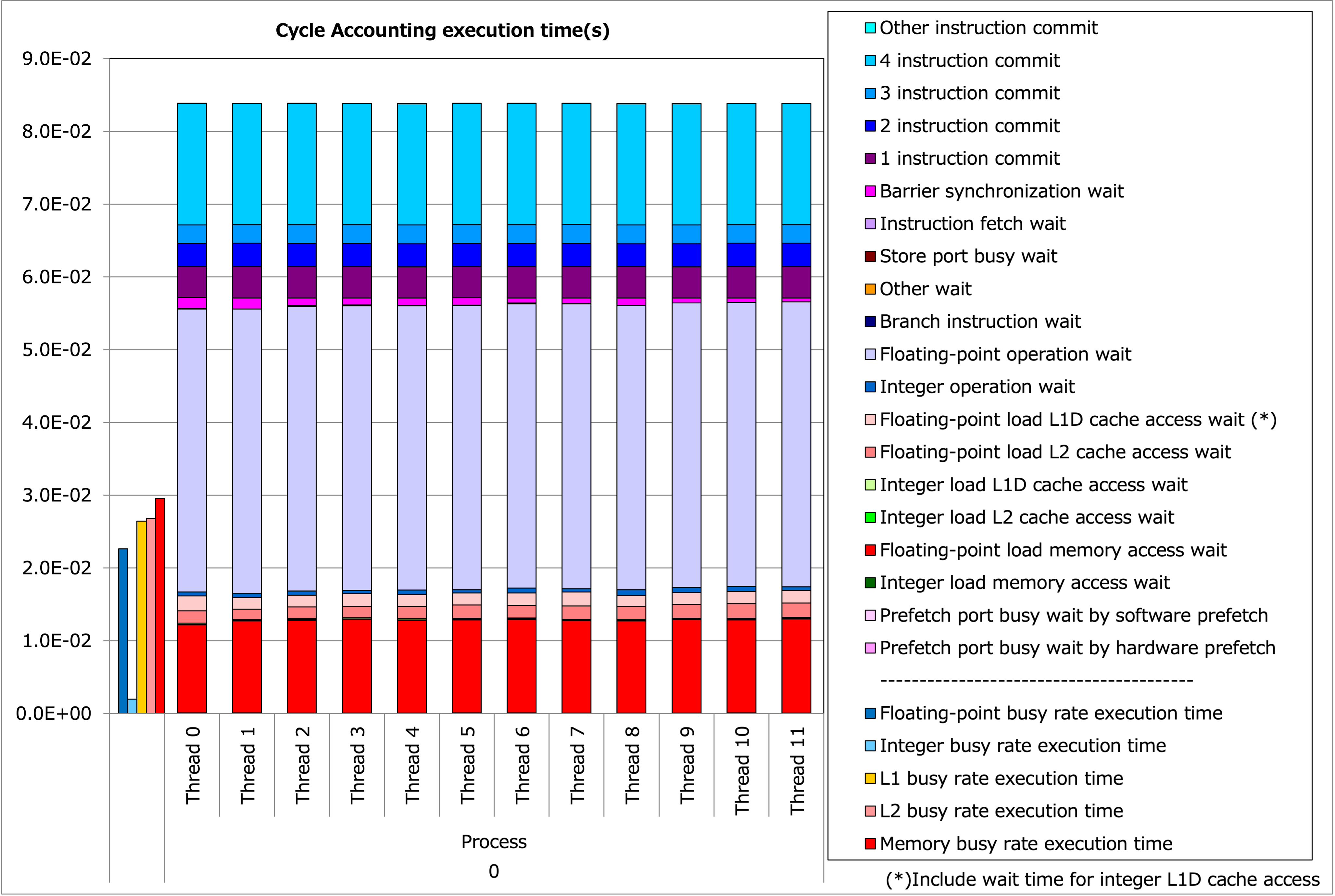
Tune-2 の実行時間内訳¶
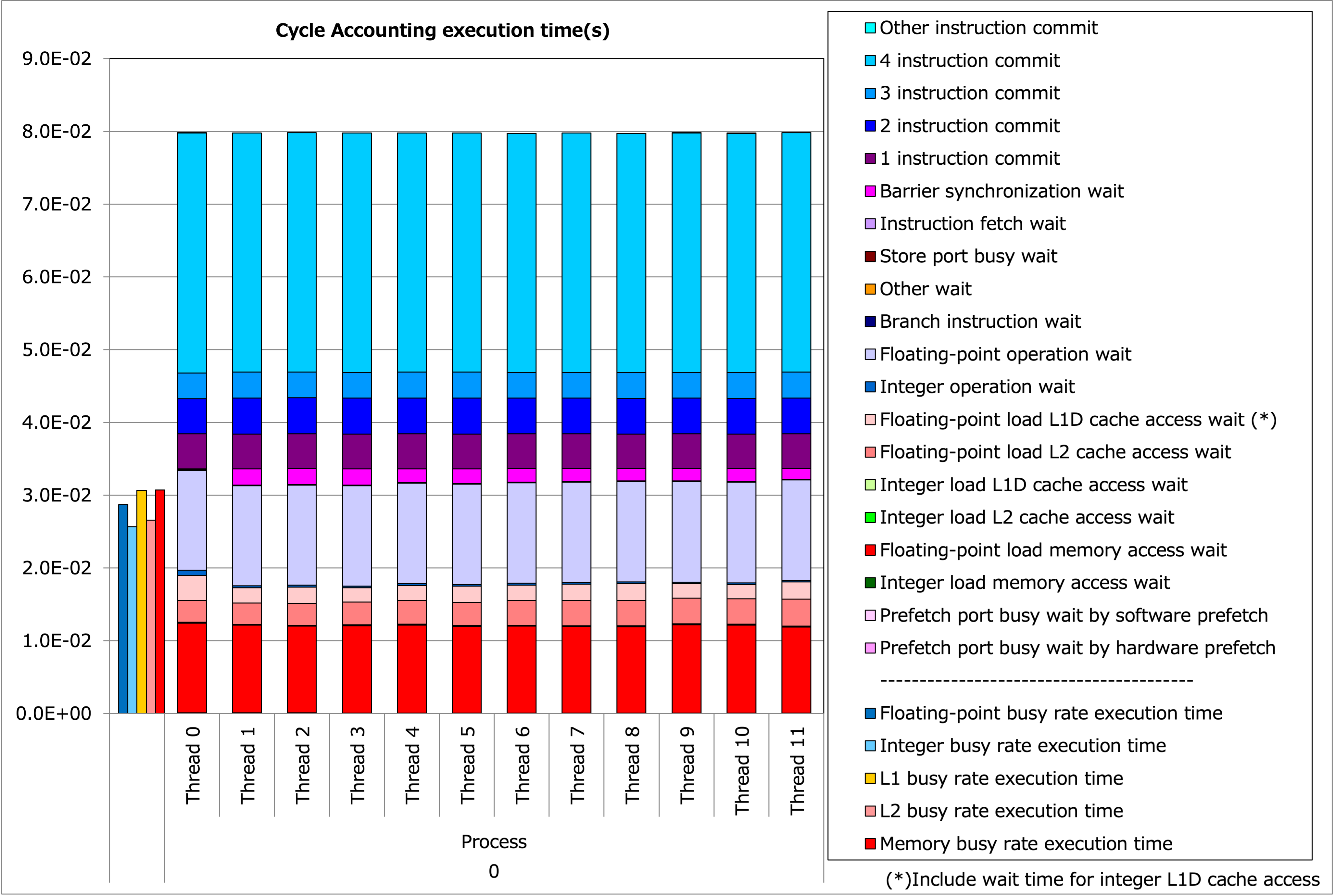
Tune-3 の実行時間内訳¶
一見薄紫色の命令待ち時間が大幅に減っているのですが、 4 命令コミットが増えており合計時間としては僅かな改善に留まります。これはソフトウェアパイプライニングされたバージョンでは特に整数命令の数が増えている為で、例えば IPC の値は 1.01→2.01 、コアあたりの GIPS の値は 2.03→4.02 となっており、ほぼ毎サイクルに 1 回の命令が増えていることがわかります。このことは決して追加のボトルネックとなってソフトウェアパイプライニングの恩恵を相殺したのではなく、浮動小数点演算の密度が微増したところに整数演算が同時実行されるようになったためと考えることができます。
スケジューリングの改善が限定的だった理由ですが、既に
tune-1
の段階でループ変数
j
に対して(長さが
8
で固定なので)フルアンロールが行われていたこと、このためある程度のスケジューリングは既に得られていたことが考えられます。必ずしも大きな効果は得られませんでしたが、ここで導入したループ
collapse
は次の
tune-4
で再び活きてきます。
プリフェッチを有効に (tune-4)¶
ここまでのコードで、若干冗長なアドレス計算が残っています。
84 for(int kj = 0; kj < p_Nq*p_Nq; ++kj) {
85 const int j = kj % p_Nq;
86 const int k = kj / p_Nq;
87
88 for(int i = 0; i < p_Nq; ++i) {
89 // const dlong id = i + j * p_Nq + k * p_Nq * p_Nq + element * p_Np;
90 const dlong gbase = element * p_Nggeo * p_Np + k * p_Nq * p_Nq + j * p_Nq + i;
91 const dfloat r_G00 = ggeo[gbase + p_G00ID * p_Np];
92 const dfloat r_G01 = ggeo[gbase + p_G01ID * p_Np];
93 const dfloat r_G11 = ggeo[gbase + p_G11ID * p_Np];
94 const dfloat r_G12 = ggeo[gbase + p_G12ID * p_Np];
95 const dfloat r_G02 = ggeo[gbase + p_G02ID * p_Np];
96 const dfloat r_G22 = ggeo[gbase + p_G22ID * p_Np];
ggeo
は多次元配列でいえば
double ggeo[Nelements][7][512]
のような次元となります(
p_Np=512
)。一度 collapse させた以上は、変数
kj
から直接アドレスを求めることができます。
84 for(int kj = 0; kj < p_Nq*p_Nq; ++kj) {
85 const int j = kj % p_Nq;
86 const int k = kj / p_Nq;
87
88 for(int i = 0; i < p_Nq; ++i) {
89 // const dlong id = i + j * p_Nq + k * p_Nq * p_Nq + element * p_Np;
90 const dlong gbase = element * p_Nggeo * p_Np + kj * p_Nq + i;
わずかな整数演算の節約に見えるのですが、 得られた性能は
606 GFLOP/s
(
tune-3
から
+62%
)と大幅に伸びています。この理由なのですが、ループ変数
kj
に直接比例して伸びるようなアドレス計算となったことでコンパイラがソフトウェアプリフェッチ命令を出すようになったことです。今回、プリフェッチ命令の出力についてはコンパイラの最適化メッセージからはその有無を確認できませんでしたが、 コンパイラの出力したアセンブリコードからは確認できます。
1313:/* 91 */ prfm 2, [x30, 824] // PLDL2KEEP for 00010
1320:/* 91 */ prfm 0, [x30, 312] // PLDL1KEEP for 00000
4324:/* 130 */ prfm 18, [x12, 760] // PSTL2KEEP for 10010
4325:/* 130 */ prfm 16, [x12, 248] // PSTL1KEEP for 10000
命令の詳細については [4] を御覧ください。
オリジナルの文献 [1] [2] では最終段のチューニングとしては手動でソフトウェアプリフェッチを挿入していましたが、今回はコンパイラによる挿入で同等のチューニングが達成できたことになります。
このバージョンのプロファイル結果は以下のようになります。
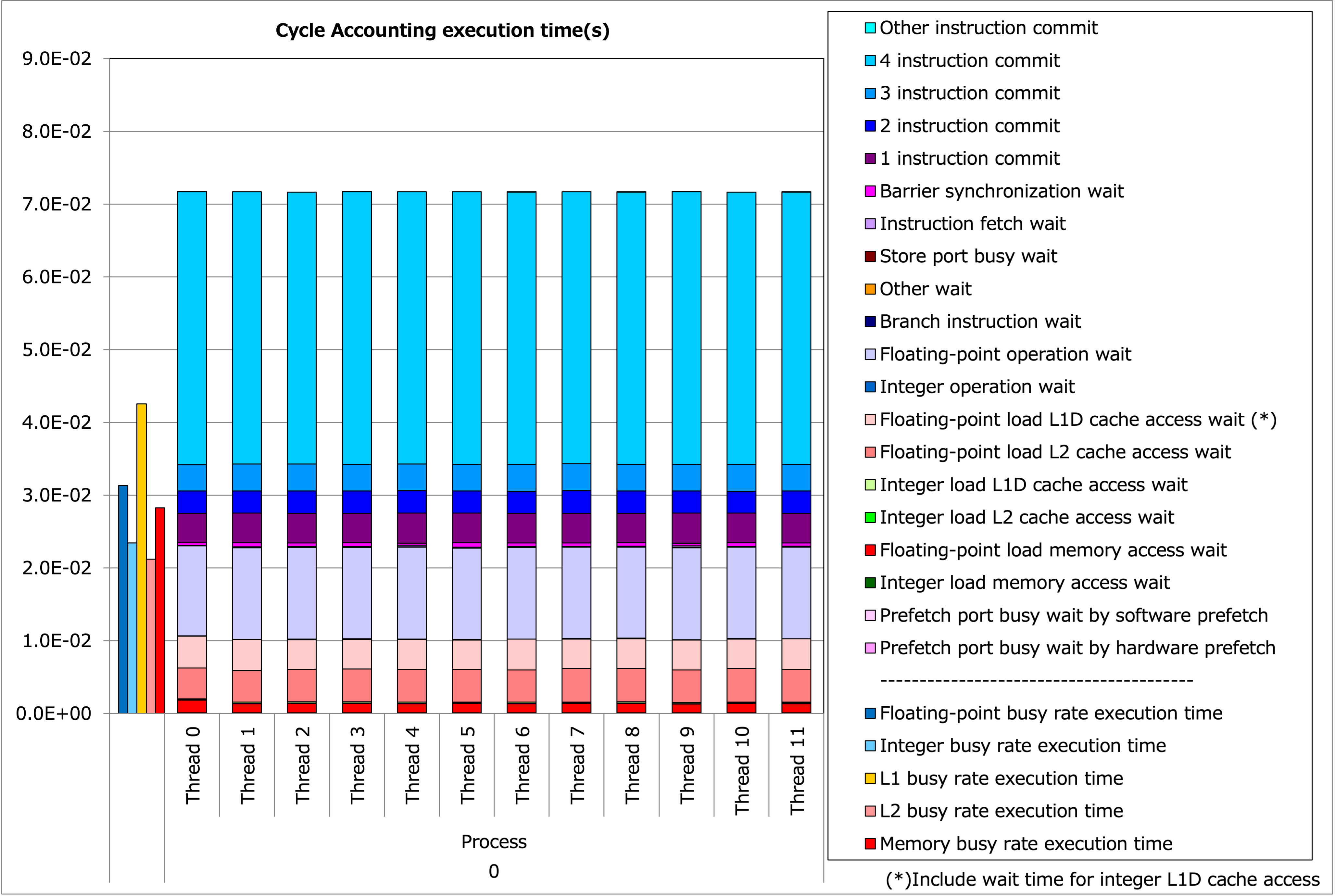
Tune-4 の実行時間内訳¶
メモリ待ち時間が改善していることが見て取れます。また、(左の赤い縦棒)のメモリビジー時間も 3.0E-02 を若干割り込むまでに減っており、プリフェッチの結果主記憶アクセスも削減できたとみなせます。
まとめ¶
ここまでカーネルと性能の一覧は以下のようになります。
カーネル |
内容 |
GFLOP/s |
tune-0 |
as-is |
126 |
tune-1 |
SIMD 化 |
329 |
tune-1a |
SIMD 化(別解) |
321 |
tune-2 |
連続アクセス |
358 |
tune-3 |
ソフトウェアパイプライニング |
374 |
tune-4 |
プリフェッチ |
606 |
特に高い効果が見られたのが、適切なループ変数による SIMD 化です。また、最後のプリフェッチも高い効果を発揮していますが、これは tune-3 で導入したループ collapse からの積み重ねで実現できたものでもあります。