2.1. Interchange of Innermost Loop with Data Dependency

2.1.1. Motivation

As the result of vectorization by compilers, calculations for different loop iterations are executed simultaneously. Therefore, in cases that there is any data dependency between loop iterations, that loop can not be vectorized because the calculation results must be obtained as written in the source program.

Program without loop-carried data dependency

DO i = 1, n
  x(i) = x(i) + 1
END DO

Program with loop-carried data dependency

DO i = 1, n
  x(i) = x(i-1) + 1
END DO

When there is no data dependency between loop iterations of an outer loop even if the innermost loop has data dependency, interchange of these loops makes it possible to vectorize the outer loop.

As a result, simultaneous execution of calculations for different loop iterations might reduce execution time.

2.1.2. Applied Example

Referring to an example presented in “Meetings for application code tuning on A64FX computer systems”, performance improvement by applying this technique is shown below. In this example, a loop for do-variable k, which has data dependency for arrays of R12pls, E12mns, R12mns and E12pls, is interchanged with loops for do-variable ich and icloud.

Original

  do ich = 1, chmax
     do icloud = 1, 2
        ic = (ich - 1) * MSTRN_ncloud + icloud
        ...
        R(rd_kmax+1) = 0
        T(rd_kmax+1) = 0
        do k = rd_kmax, 1, -1
           R(k) = (cf(k)) * R0(k,I_Cloud,ich) &
                + (1.0_RP - cf(k)) * R0(k,I_ClearSky,ich)
           T(k) = (cf(k)) * T0(k,I_Cloud,ich) &
                + (1.0_RP - cf(k)) * T0(k,I_ClearSky,ich)
           R12pls(k,ic) = R(k) + T(k) / (1.0_RP - R12pls(k+1,ic) * R(k)) &
                * (R12pls(k+1,ic) * T(k))
           E12mns(k,ic) = Em(k,ic) + T(k) / ( 1.0_RP - R12pls(k+1,ic) * R(k)) &
                * (R12pls(k+1,ic) * Ep(k,ic) + E12mns(k+1,ic))
        end do
        do k = 2, rd_kmax+1
           R12mns(k,ic) = R(k) + T(k) / (1.0_RP - R12mns(k-1,ic) * R(k)) &
                * (R12mns(k-1,ic) * T(k))
           E12pls(k,ic) = Ep(k,ic) + T(k) / (1.0_RP - R12mns(k-1,ic) * R(k)) &
                * (R12mns(k-1,ic) * Em(k,ic) + E12pls(k-1,ic))
        end do
     end do
  end do

Technique applied

  do ich = 1, chmax
     do icloud = 1, 2
        ic = (ich - 1) * MSTRN_ncloud + icloud
        do k = 1, rd_kmax
           R(k,ic) = (cf(k,ic)) * R0(k,I_Cloud,ich) &
                + (1.0_RP - cf(k,ic)) * R0(k,I_ClearSky,ich)
           T(k,ic) = (cf(k,ic)) * T0(k,I_Cloud,ich) &
                + (1.0_RP - cf(k,ic)) * T0(k,I_ClearSky,ich)
        end do
        R(rd_kmax+1,:) = 0
        T(rd_kmax+1,:) = 0
     end do
  end do
  do kk = 1, rd_kmax
     do ic = 1, chmax * MSTRN_ncloud
        k = rd_kmax - kk + 1
        R12pls(ic,k) = R(k,ic) + T(k,ic) / (1.0_RP - R12pls(ic,k+1) * R(k,ic)) &
             * (R12pls(ic,k+1) * T(k,ic))
        E12mns(ic,k) = Em(k,ic) + T(k,ic) / (1.0_RP - R12pls(ic,k+1) * R(k,ic)) &
             * (R12pls(ic,k+1) * Ep(k,ic) + E12mns(ic,k+1))
        k = kk + 1
        R12mns(ic,k) = R(k,ic) + T(k,ic) / (1.0_RP - R12mns(ic,k-1) * R(k,ic)) &
             * (R12mns(ic,k-1) * T(k,ic))
        E12pls(ic,k) = Ep(k,ic) + T(k,ic) / (1.0_RP - R12mns(ic,k-1) * R(k,ic)) &
             * (R12mns(ic,k-1) * Em(k,ic) + E12pls(ic,k-1))
     end do
  end do

Ratios of SIMD instructions and results of cycle accounting for executions before/after applying the technique are shown in graphs below. Parameters for the loop execution are as follows:

rd_kmax = 54, chmax = 5, MSTRN_ncloud = 2

Comparing the lower graph for the technique applied to the upper graph for the original, ratio of SIMD instructions was improved from 0% to 38% and execution time was reduced by 67%.

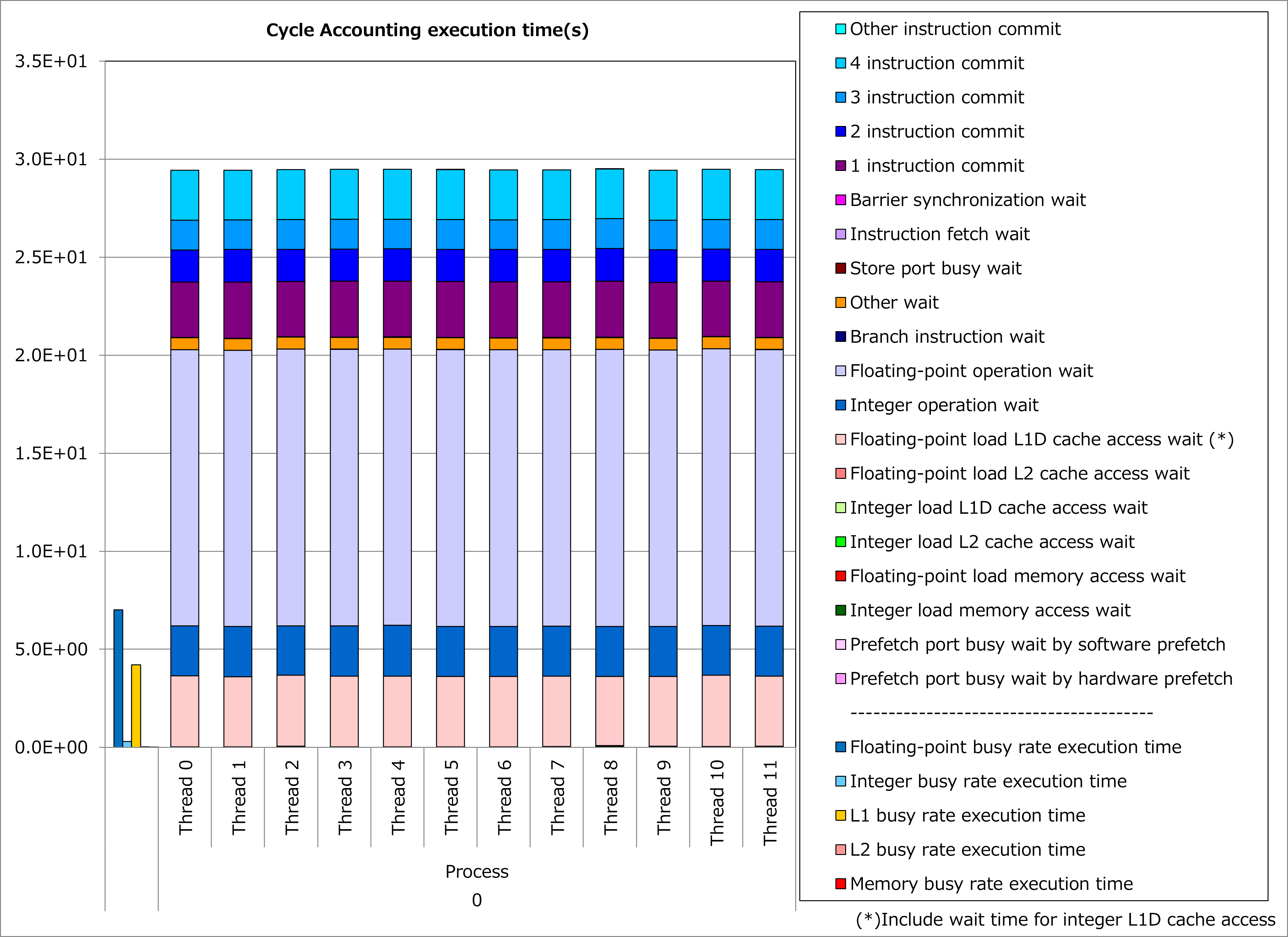
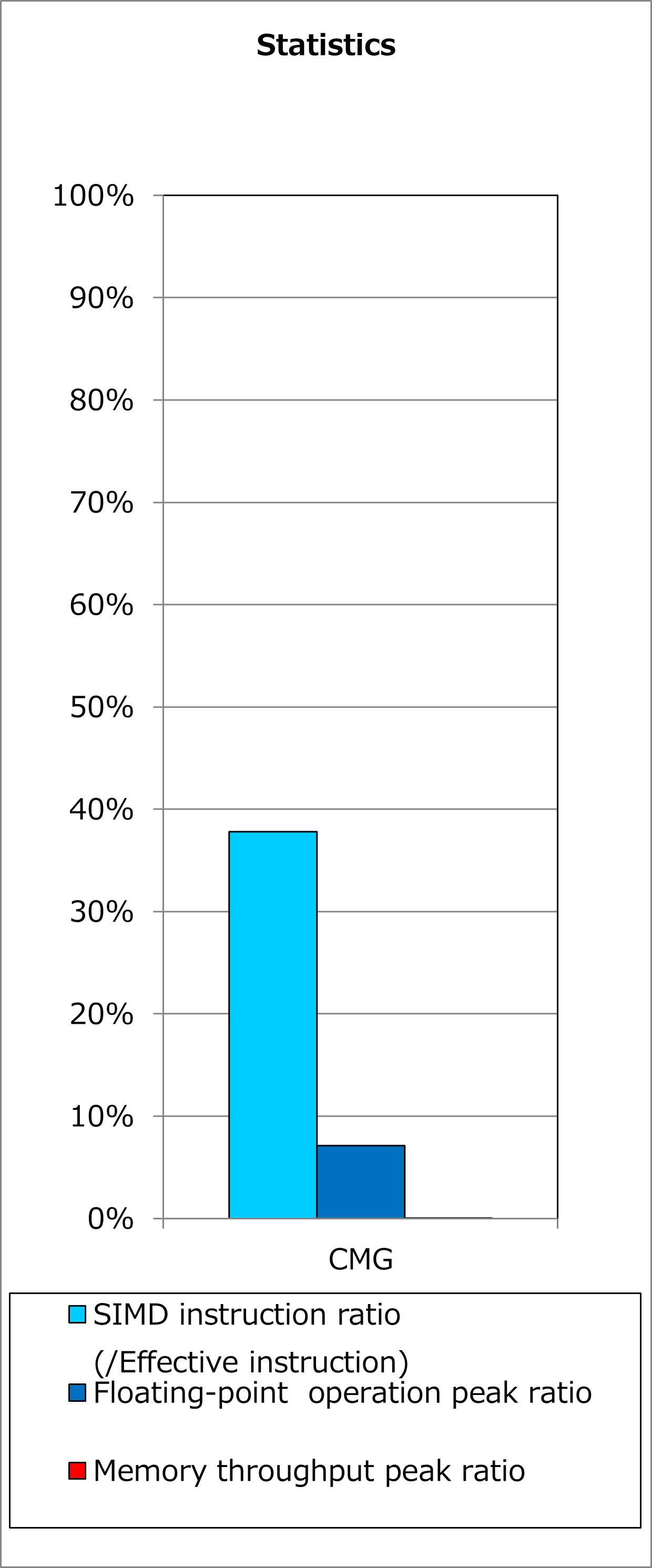
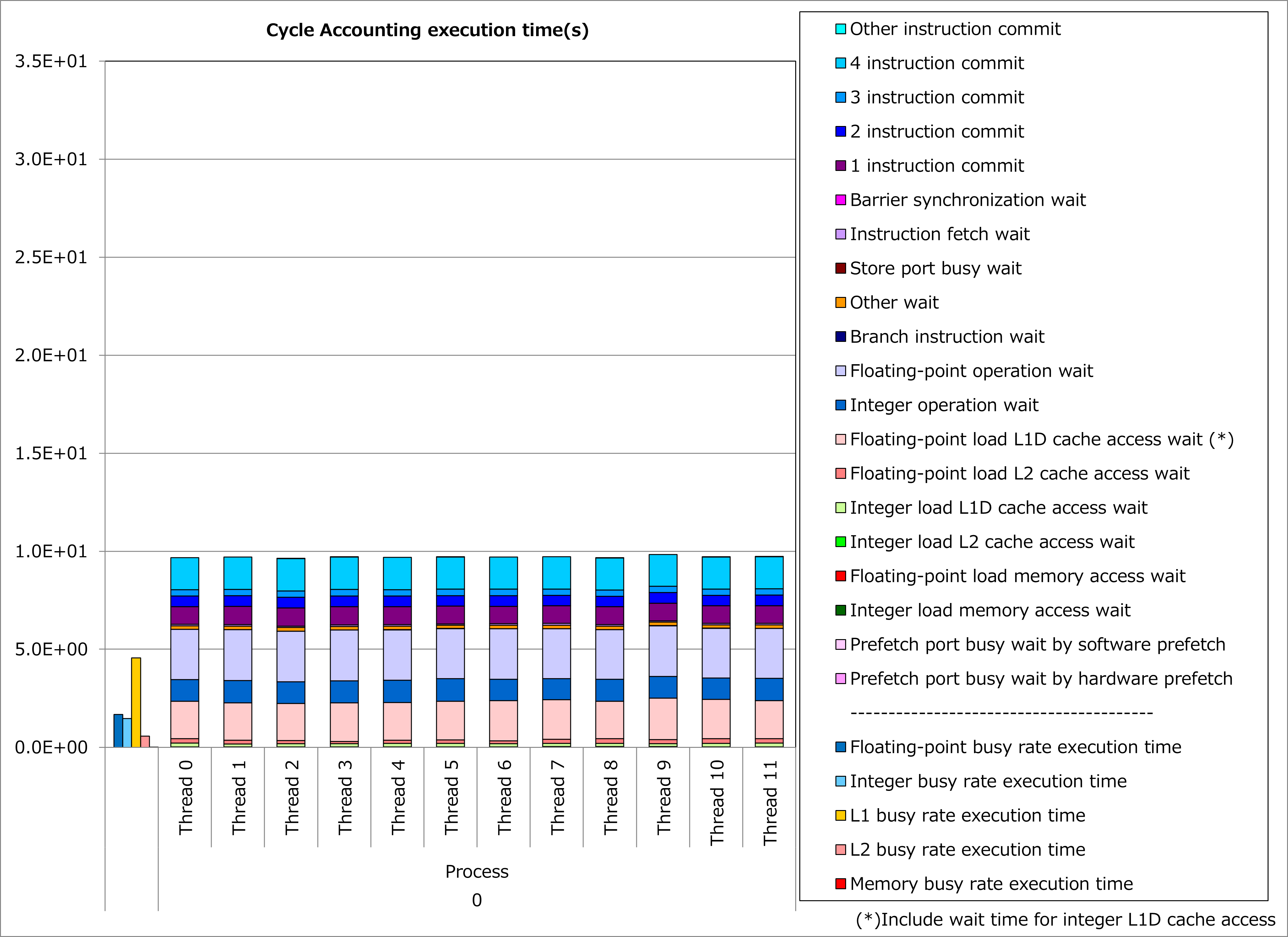
2.1.3. Real Cases

A real case related to this technique is presented in “Meetings for application code tuning on A64FX computer systems” as follows:

• A64FX Tuning - SCALE on Fugaku -